Procedural Skydomes on the Web

Ever since I've been exploring 3D graphics, I've been veering into game development and realtime graphics, particularly on the web. Exploring this has shown me the importance of skyboxes and skydomes. When building virtual worlds, having a skydome adds to the immersion of a scene by introducing a sort of backdrop. With that said, it's probably easier to show than tell.

Let's say I want an outdoor scene that takes place during the day. Just to quickly set up the scene, here's a ground plane we can get started with.

Drag around the image to look around!

There's not much else there, and as a matter of fact the background of the scene is the background of this webpage. Let's add a sphere to work as our skydome. I'm gonna add a sphere, scale it up really big, and make the faces point inward so that we can see it from the inside. Let's go with a softer color palette too.

Okay, now we have some semblance of a sky and horizon. Now, most clear skies are actually a blend of at least two colors: one near the horizon blends into others higher in the sky. Take a look at this real-world example.

A roadside scene in the farmlands of Drummond, Idaho. Most apparent in the photo is the gradient between a deep blue and sky blue at the horizon
Image courtesy: Cate Bligh

Notice how the sky is composed of a deep blue high in the sky and a softer blue near the horizon? If you look at any horizon at any time of day, you can see a gradient of two, three, and sometimes four colors. Now that we know this, we need our skydome to smoothly blend between two colors. We can do this using some GLSL shaders, thanks to WebGL.

I'll save the basics of how these shaders work for another article, but I'll try my best to explain some high level stuff as we go. Basically, we want the color of our skydome sphere to change according to where on the sphere we are. At the top of the sphere, we want to be one color, and at the bottom we want to be another. As we move down the sphere, the colors should smoothly blend between each other. To do this, we write a fragment shader so that we can get the UV position of any part of the sphere.

Here, we define a variable v to keep track of where we are along the height of the sphere. Its value will be 0 at the very bottom of the sphere and 1 at the very top. We make it varying, because we'll be using it in our fragment shader to decide the colors of the sphere.

Now, for a basic gradient we just use v to linearly interpolate between our horizon color and sky color.

Here, horizonColor is the color at the horizon and skyColor is the color high in the sky. Let's see how this looks.

Huh. We can barely see a difference between this and our last scene. Why is that? Well, it's because our gradient is so smooth and our sphere is so big that it's really hard for us to even see any change in color. We can only see half of the gradient anyway, since half of the sphere is below the ground plane.

To make our dome more realistic, we need to control where and how quickly the color blending occurs. If our v variable from earlier is 0 at the bottom of the sphere and 1 at the top, how can we modify that to control where and when 0 goes to 1? Luckily, there's a nice set of mathematical functions that we can use to do this called Sigmoid functions.

We'll use an algebraic sigmoid function for this job, since we can tweak it to our needs and it's not too computationally intensive.

dax−bc+(ax−b)2+ed\frac{ax-b}{\sqrt{c + (ax-b)^2}} + e
Put this function in a graphing calculator and mess with the parameters to change the curve's shape.

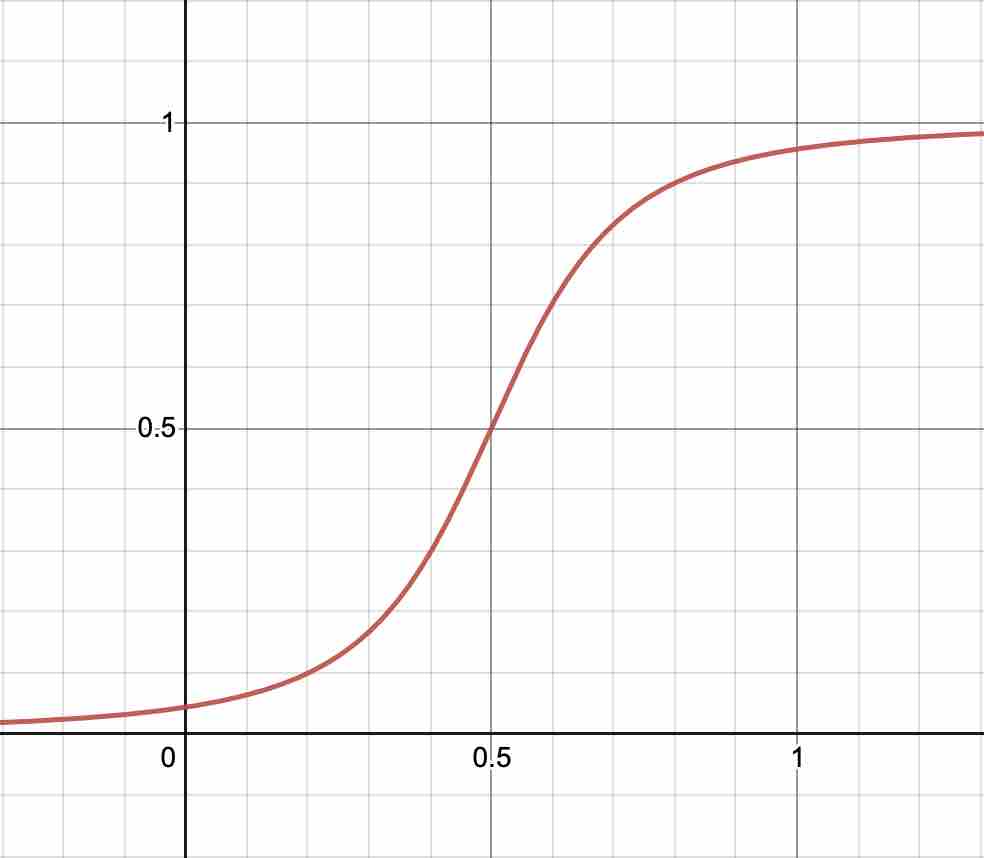
Remember algebra from school. We can use d to control the height of the function, b to control its shift along the horizontal axis, and e to control its shift along the vertical axis. a and c control the actual shape of the S-curve.

For example, this is what the curve looks like when a is 1, c is 0.05, and b, d and e are 0.5.

The algebraic sigmoid curve with said parameters
Notice how most of the action in the function takes place between 0 and 1 on both axes, which is great for our use in GLSL.

But who care's about the math right? Let's just put this into some code, give some parameters to shape our curve, and see what we get. Doing just that, here's our new fragment shader.

Here, we're implementing the algebraic sigmoid in GLSL and then making a function called horizonCurve that defines some parameters of the curve. We then use the shape of the horizon curve to interpolate between the horizon color and sky color. Here's how it looks.

It's so much more natural-looking! And the best part is that, because it's procedural, we can change the colors whenever we want to whatever colors we want. Let's add a day cycle, where we can change the sky colors according to the time of day. Hit a button to change to that time of day.

And while we're here, why not add a sun / moon just because? Maybe even some bloom for a bit of that ✨dreamy✨ feel.

And there we go! To add a realtime skydome to your 3D scene, add a sphere, blow it up really big, point the faces inward and then do some shader tricks involving some clever math. Once that's done it's up to you to pick colors and postprocessing to get the look you want. And the best part is that we can get somewhat close to photorealism without modeling real-world light and atmospheric patterns.